Monty Hall Problem Simulator

मॉन्टी हॉलची समस्या संभाव्यता सिद्धांताच्या व्याप्तीमध्ये सर्वात प्रसिद्ध गणितीय समस्या आहे:

टेलिव्हिजनवरील गेम शोमध्ये होस्टने प्लेअरच्या समोर असलेल्या तीन बंद दारेपैकी एक निवडण्यासाठी खेळाडूला विचारतो. दोन दरवाजे मागे बकर्या आहेत आणि एक दरवाजा मागे एक गाडी आहे ज्याने तो दार लावताना खेळाडू विजयी होऊ शकतो. खेळाडूने एक दरवाजा निवडला (नंतर बंद राहतो), होस्ट दुसर्या बॉलला उघडतो ज्यात त्याच्या मागे बकरी आहे. यजमान नंतर खेळाडूला दरवाजावर थांबू इच्छितो की त्याने सुरुवातीला निवड केली आहे किंवा इतर बंद दरवाजावर जायचे आहे.

प्रश्न हे स्पष्टपणे आहे: खेळाडूने दरवाजा बंद केला पाहिजे किंवा निवडलेल्या दरवाजावर थांबला पाहिजे का?

बरेच लोक असे म्हणतील की खेळाडू दार बंद करतो की नाही हे काही फरक पडत नाही, कारण कार जिंकण्याची संभाव्यता 50/50 आहे तरीही. जरी हे योग्य वाटत असले तरी दोन समान बंद दरवाजे आहेत, हे चुकीचे आहे.

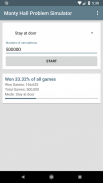
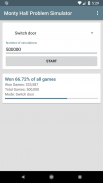
योग्य उत्तर म्हणजे कार जिंकण्याची संधी 67% आहे जेव्हा खेळाडू दार लावून घेतो आणि केवळ 33% जेव्हा खेळाडूने दरवाजाजवळ थांबून पहिल्यांदा निवडले आहे.

अद्याप भेटले विश्वास नाही? फक्त अॅप डाउनलोड करा आणि हे वापरून पहा!

हा अॅप आपल्याला सलगपणे 5 दशलक्ष वेळा पर्यंत वर्णित गेम परिसर अनुकरण करण्यास अनुमती देतो. आपण प्रथम नेहमी निवडलेला दरवाजा स्विच करावा किंवा नेहमी दारवर कायम राहण्यासाठी आपण सिम्युलेटेड प्लेअरला हवे ते निवडू शकता. अॅप्पने गेमची विनंती केलेली संख्या अनुकरण केल्यानंतर, हे आपल्याला आकडेवारी देते जे आपल्याला किती खेळाडूंनी जिंकले आहे हे दिसून येते. या प्रकारे आपण खेळाडू दरवाजा स्विच किंवा पाहिजे नये किंवा नाही हे सांगू शकता.